DiCoDiLe on the Mandrill image

This example illlustrates reconstruction of Mandrill image using DiCoDiLe algorithm with default soft_lock value “border” and 9 workers.

import numpy as np
import matplotlib.pyplot as plt

from dicodile.data.images import fetch_mandrill

from dicodile.utils.dictionary import init_dictionary
from dicodile.utils.viz import display_dictionaries
from dicodile.utils.csc import reconstruct

from dicodile import dicodile

We will first download the Mandrill image.

X = fetch_mandrill()

plt.axis('off')
plt.imshow(X.swapaxes(0, 2))

Downloading data from https://sipi.usc.edu/database/download.php?vol=misc&img=4.2.03 (1 byte)


file_sizes:   0%|                                    | 0.00/1.00 [00:00<?, ?B/s]
file_sizes: 32.8kB [00:00, 206kB/s]
file_sizes: 213kB [00:00, 745kB/s]
file_sizes: 787kB [00:00, 1.94MB/s]
Successfully downloaded file to /github/home/data/dicodile/images/standard_images/mandrill_color.tif

<matplotlib.image.AxesImage object at 0x7f8a2a87d7f0>

We will create a random dictionary of K = 25 patches of size 8x8 from the original Mandrill image to be used for sparse coding.

# set dictionary size
n_atoms = 25

# set individual atom (patch) size
atom_support = (8, 8)

D_init = init_dictionary(X, n_atoms, atom_support, random_state=60)

We are going to run dicodile with 9 workers on 3x3 grids.

# number of iterations for dicodile
n_iter = 3

# number of iterations for csc (dicodile_z)
max_iter = 10000

# number of splits along each dimension
w_world = 3

# number of workers
n_workers = w_world * w_world

Run dicodile.

D_hat, z_hat, pobj, times = dicodile(X, D_init, n_iter=n_iter,
                                     n_workers=n_workers,
                                     dicod_kwargs={"max_iter": max_iter},
                                     verbose=6)


print("[DICOD] final cost : {}".format(pobj))

[DEBUG:DICODILE] Lambda_max = 11.274413430904202
Started 9 workers in 3.71s
[INFO:DICODILE] - CD iterations 0 / 3 (0s)
[DEBUG:DICODILE] lambda = 1.127e+00

[INFO:DICOD-9] converged in 277.705s (187.885s) with 9342673 iterations (1084324 updates).
[DEBUG:DICODILE] Objective (z) : 3.272e+04 (279s)

[PROGRESS:Update D] 1s -   4.00% iterations (7.921e-05)
[PROGRESS:Update D] 1s -   5.00% iterations (7.921e-05)
[PROGRESS:Update D] 1s -   6.00% iterations (7.921e-05)
[PROGRESS:Update D] 1s -   7.00% iterations (7.921e-05)
[PROGRESS:Update D] 1s -   8.00% iterations (7.921e-05)
[PROGRESS:Update D] 1s -   9.00% iterations (7.921e-05)
[PROGRESS:Update D] 1s -  10.00% iterations (7.921e-05)
[PROGRESS:Update D] 2s -  11.00% iterations (7.921e-05)
[PROGRESS:Update D] 2s -  12.00% iterations (7.921e-05)
[PROGRESS:Update D] 2s -  13.00% iterations (7.921e-05)
[PROGRESS:Update D] 2s -  14.00% iterations (7.921e-05)
[PROGRESS:Update D] 2s -  15.00% iterations (7.921e-05)
[PROGRESS:Update D] 2s -  16.00% iterations (7.921e-05)
[PROGRESS:Update D] 2s -  17.00% iterations (7.921e-05)
[PROGRESS:Update D] 2s -  18.00% iterations (7.921e-05)
[PROGRESS:Update D] 2s -  19.00% iterations (7.921e-05)
[PROGRESS:Update D] 2s -  20.00% iterations (7.921e-05)
[PROGRESS:Update D] 2s -  21.00% iterations (7.921e-05)
[PROGRESS:Update D] 2s -  22.00% iterations (7.921e-05)
[PROGRESS:Update D] 2s -  23.00% iterations (7.921e-05)
[PROGRESS:Update D] 3s -  24.00% iterations (7.921e-05)
[PROGRESS:Update D] 3s -  25.00% iterations (7.921e-05)
[PROGRESS:Update D] 3s -  26.00% iterations (7.921e-05)
[PROGRESS:Update D] 3s -  27.00% iterations (7.921e-05)
[PROGRESS:Update D] 3s -  28.00% iterations (7.921e-05)
[PROGRESS:Update D] 3s -  29.00% iterations (7.921e-05)
[PROGRESS:Update D] 3s -  30.00% iterations (7.921e-05)
[PROGRESS:Update D] 3s -  31.00% iterations (7.921e-05)
[PROGRESS:Update D] 3s -  32.00% iterations (7.921e-05)
[PROGRESS:Update D] 3s -  33.00% iterations (7.921e-05)
[PROGRESS:Update D] 3s -  34.00% iterations (7.921e-05)
[PROGRESS:Update D] 3s -  35.00% iterations (7.921e-05)
[PROGRESS:Update D] 3s -  36.00% iterations (7.921e-05)
[PROGRESS:Update D] 3s -  37.00% iterations (7.921e-05)
[PROGRESS:Update D] 3s -  38.00% iterations (7.921e-05)
[PROGRESS:Update D] 4s -  39.00% iterations (7.921e-05)
[PROGRESS:Update D] 4s -  40.00% iterations (7.921e-05)
[PROGRESS:Update D] 4s -  41.00% iterations (7.921e-05)
[PROGRESS:Update D] 4s -  42.00% iterations (7.921e-05)
[PROGRESS:Update D] 4s -  43.00% iterations (7.921e-05)
[PROGRESS:Update D] 4s -  44.00% iterations (7.921e-05)
[PROGRESS:Update D] 4s -  45.00% iterations (7.921e-05)
[PROGRESS:Update D] 4s -  46.00% iterations (7.921e-05)
[PROGRESS:Update D] 4s -  47.00% iterations (7.921e-05)
[PROGRESS:Update D] 4s -  48.00% iterations (7.921e-05)
[PROGRESS:Update D] 4s -  49.00% iterations (8.369e-06)
[INFO:Update D]: 50 iterations
[DEBUG:DICODILE] Objective (d) : 3.257e+04  (10s)
[INFO:DICODILE] - CD iterations 1 / 3 (291s)
[DEBUG:DICODILE] lambda = 1.127e+00

[INFO:DICOD-9] converged in 76.387s (56.902s) with 2567144 iterations (310943 updates).
[DEBUG:DICODILE] Objective (z) : 3.250e+04 (86s)

[PROGRESS:Update D] 1s -   5.00% iterations (1.360e-04)
[PROGRESS:Update D] 1s -   6.00% iterations (1.360e-04)
[PROGRESS:Update D] 1s -   7.00% iterations (1.360e-04)
[PROGRESS:Update D] 1s -   8.00% iterations (1.360e-04)
[PROGRESS:Update D] 1s -   9.00% iterations (1.360e-04)
[PROGRESS:Update D] 1s -  10.00% iterations (1.360e-04)
[PROGRESS:Update D] 1s -  11.00% iterations (1.360e-04)
[PROGRESS:Update D] 2s -  12.00% iterations (1.360e-04)
[PROGRESS:Update D] 2s -  13.00% iterations (1.360e-04)
[PROGRESS:Update D] 2s -  14.00% iterations (1.360e-04)
[PROGRESS:Update D] 2s -  15.00% iterations (1.360e-04)
[PROGRESS:Update D] 2s -  16.00% iterations (1.360e-04)
[PROGRESS:Update D] 2s -  17.00% iterations (1.360e-04)
[PROGRESS:Update D] 2s -  18.00% iterations (1.360e-04)
[PROGRESS:Update D] 2s -  19.00% iterations (1.360e-04)
[PROGRESS:Update D] 2s -  20.00% iterations (1.360e-04)
[PROGRESS:Update D] 2s -  21.00% iterations (1.360e-04)
[PROGRESS:Update D] 2s -  22.00% iterations (1.360e-04)
[PROGRESS:Update D] 2s -  23.00% iterations (6.801e-05)
[PROGRESS:Update D] 2s -  24.00% iterations (3.400e-05)
[INFO:Update D]: 25 iterations
[DEBUG:DICODILE] Objective (d) : 3.248e+04  (8s)
[INFO:DICODILE] - CD iterations 2 / 3 (387s)
[DEBUG:DICODILE] lambda = 1.127e+00

[INFO:DICOD-9] converged in 46.696s (33.956s) with 1357615 iterations (197555 updates).
[DEBUG:DICODILE] Objective (z) : 3.246e+04 (57s)

[PROGRESS:Update D] 1s -   4.00% iterations (1.361e-04)
[PROGRESS:Update D] 1s -   5.00% iterations (1.361e-04)
[PROGRESS:Update D] 1s -   6.00% iterations (1.361e-04)
[PROGRESS:Update D] 1s -   7.00% iterations (1.361e-04)
[PROGRESS:Update D] 1s -   8.00% iterations (1.361e-04)
[PROGRESS:Update D] 1s -   9.00% iterations (1.361e-04)
[PROGRESS:Update D] 1s -  10.00% iterations (1.361e-04)
[PROGRESS:Update D] 2s -  11.00% iterations (1.361e-04)
[PROGRESS:Update D] 2s -  12.00% iterations (1.361e-04)
[PROGRESS:Update D] 2s -  13.00% iterations (1.361e-04)
[PROGRESS:Update D] 2s -  14.00% iterations (1.361e-04)
[PROGRESS:Update D] 2s -  15.00% iterations (1.361e-04)
[PROGRESS:Update D] 2s -  16.00% iterations (6.805e-05)
[PROGRESS:Update D] 2s -  17.00% iterations (1.798e-06)
[INFO:Update D]: 18 iterations
[DEBUG:DICODILE] Objective (d) : 3.245e+04  (8s)

[INFO:DICOD-9] converged in 35.968s (26.217s) with 1262628 iterations (139458 updates).
[INFO:DICODILE] Finished in 450s
[DICOD] final cost : [115793.6905497883, 32716.28216140542, 32567.301367286178, 32503.06630871378, 32484.71520026442, 32457.331542500335, 32449.88390265819, 32433.63225171788]

Plot and compare the initial dictionary D_init with the dictionary D_hat improved by dicodile.

# normalize dictionaries
normalized_D_init = D_init / D_init.max()
normalized_D_hat = D_hat / D_hat.max()

display_dictionaries(normalized_D_init, normalized_D_hat)

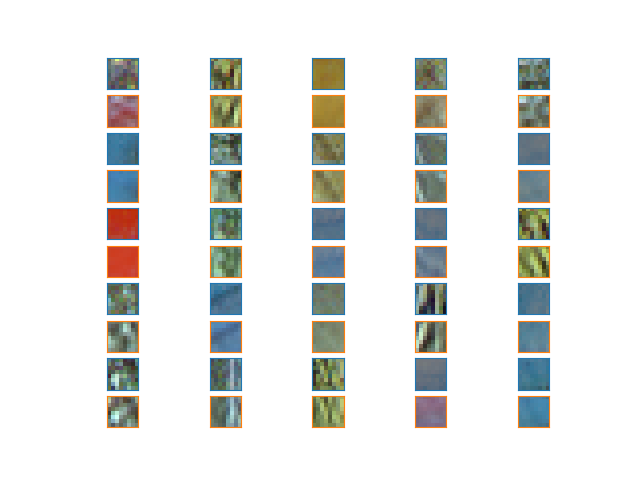
<Figure size 640x480 with 50 Axes>

Reconstruct the image from z_hat and D_hat.

X_hat = reconstruct(z_hat, D_hat)
X_hat = np.clip(X_hat, 0, 1)

Plot the reconstructed image.

fig = plt.figure("recovery")

ax = plt.subplot()
ax.imshow(X_hat.swapaxes(0, 2))
ax.axis('off')
plt.tight_layout()